Study notes on regular expressions and finite state automata

My first encounter with regular expressions (regex) involved writing a rule to search for email addresses. I started by watching a tutorial, then gave up and went to StackOverflow until I found this expression:

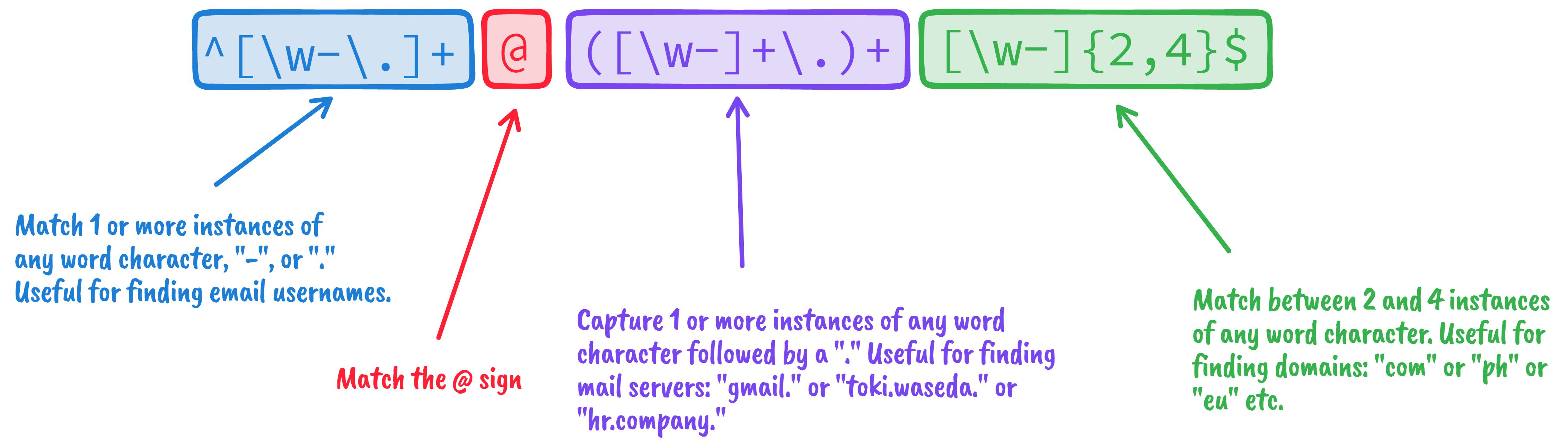
I know better now that I can write regex for simple cases, but still, these patterns feel like sorcery. Little did I know that they’ll be back to haunt me. This time, in linguistics.

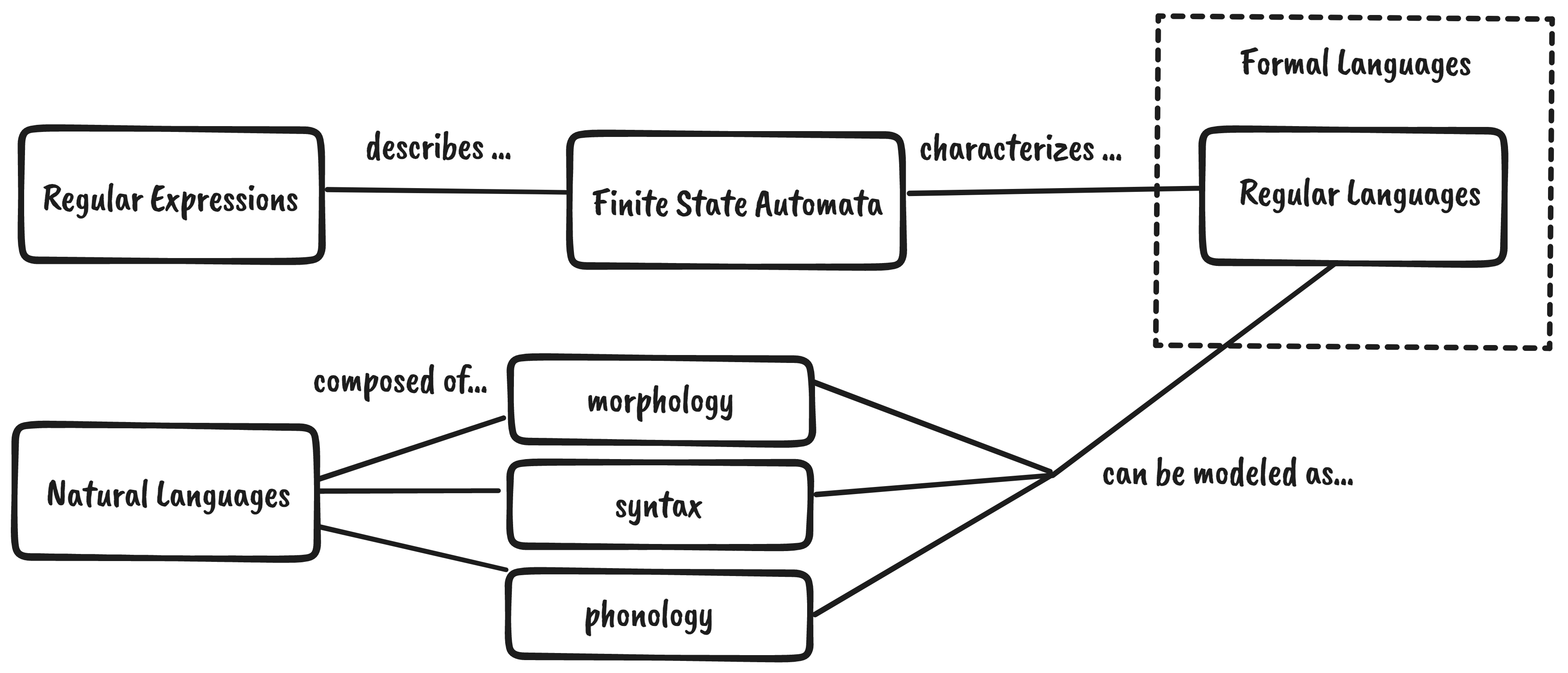
As it turns out, we can use regular expressions to characterize certain aspects of natural language such as their morphology (word structure), syntax, and phonology (sound). We can do so by representing regex as a finite-state automaton (FSA).¹

Regular expressions as finite state automata

Let’s start with a simple and contrived example. Say we want to model the language of sheep, Sheeptalk. Based from our field research, sheep can speak the following lines:

baa!
baaaaa!
baaaaaaaa!
baaa!

There’s not much variety here. Fortunately for us, we can model the entirety of Sheeptalk with this simple regular expression, baa+!:

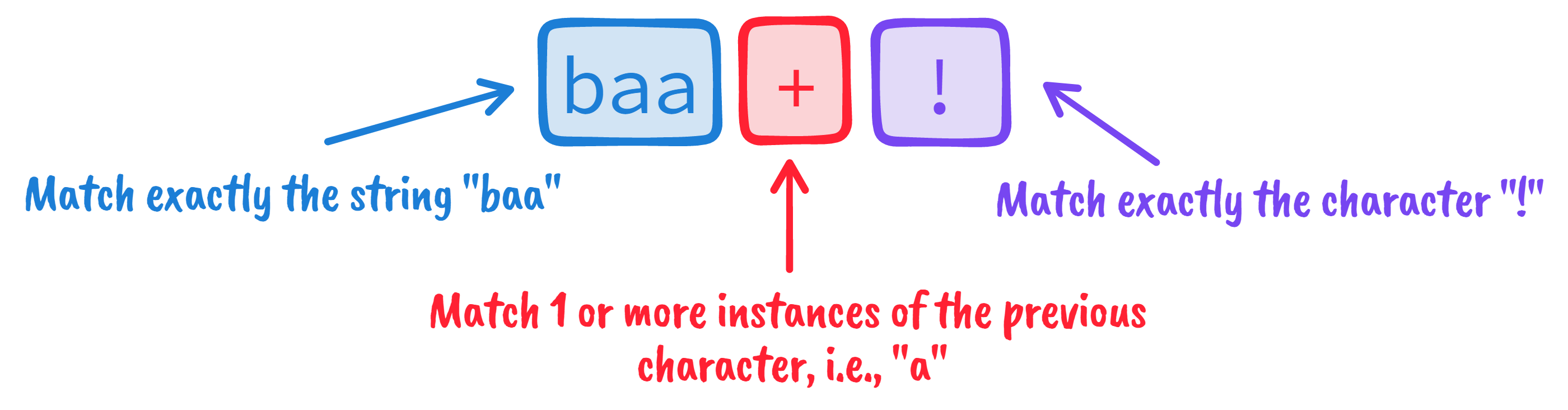
As we’ll see later, regex isn’t just a metalanguage for searching and matching strings. It also describes a finite state automaton (FSA) that can recognize if a set of input strings correspond to an instance of our language. So, for example, we can use that FSA to check if a given string, say “baa!” or “meow,” is an instance of Sheeptalk.

We can use a finite state automaton (FSA) to recognize if a set of input correspond to an instance of our regular language. For example, we can use FSA to check if a given string, say “baa!” or “meow,” is an instance of Sheeptalk.

Recall that finite state machines are represented by states and their transitions. We usually draw them as a directed graph, where the states are denoted by nodes, and transitions by their vertices. The FSA equivalent of Sheeptalk is seen below:

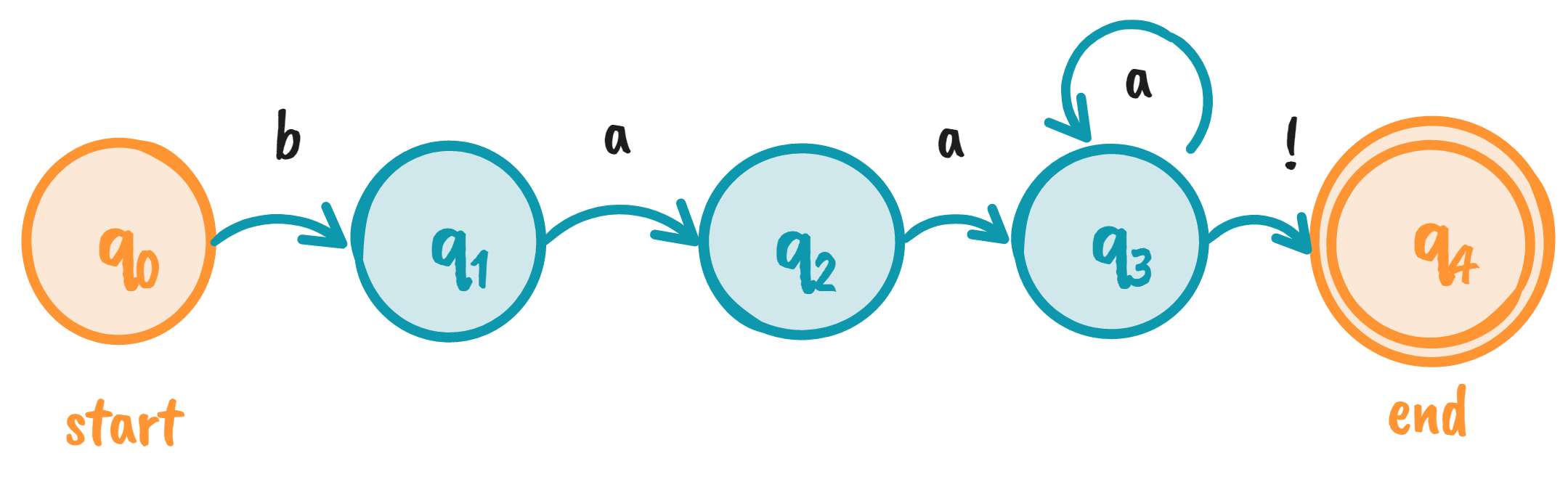
We have a five states from \(q_0\) to \(q_4\), where \(q_0\) is the start state and \(q_4\) is the end / accept state.
We assign characters for each transition. As we’ll see in a later section, these transition arcs don’t have to be characters. They can be any symbol.

[Definition] Formally, we define an FSA as the following :

\[A = (Q, \Sigma, q_0, F, \delta(q, i))\]

where:

\(Q\): is a finite set of \(N\) states (\(\{q_0,q_1,q_2,q_3,q_4\}\))
\(\Sigma\): finite input alphabet of symbols (\(\{a, b, !\}\))
\(q_0\): the designated start state (\(q_0\))
\(F\): the set of final states, \(F\subseteq Q\) (\(F=\{q_4\}\))
\(\delta(q,i)\): the transition function, will be discussed in the next section

The transition function

The transition function \(\delta(q,i)\) is the heart of an FSA. It defines what happens when the FSA encounters a specific state \(q\) and specific symbol \(i\). It then returns the next state \(q'\). Formally, we define it as:

\(\delta: Q \times \Sigma \rightarrow Q\): the transition function is defined on a set of states \(Q\) and a set of input symbols \(\Sigma\), then maps (\(\rightarrow\)) to a set of states \(Q\).
\(\delta(q,i) = q'~\text{for}~q, q' \in Q, i \in \Sigma\): when the transition function is applied to a specific state and symbol, \(\delta(q, i)\), it gives us the next state \(q'\) which of course is an element of \(Q\).

In code, Sheeptalk’s transition function can be written as:

from typing import Union

def delta(q: str, i: str) -> Union[str, None]:
    transition_table = {
        # q, i -> q'
        ("q0", "b"): "q1", 
        ("q1", "a"): "q2", 
        ("q2", "a"): "q3", 
        ("q3", "a"): "q3", 
        ("q3", "!"): "q4", 
    }
    return transition_table.get((q, i), None)

We return a None value if the input combination is invalid. Note that this is just a simple implementation of a transition table. In Python, you can use libraries such as pyfst for complex tables. Now that we have a delta function, we can use it by supplying the current state q and current input i:

delta(("q0", "b"))  # returns "q1"
delta(("q3", "a"))  # returns "q3"
delta(("q0", "a"))  # returns None 

Putting it all together

Below is an implementation for the Sheeptalk FSA. I implemented it as a class to easily attach utility functions useful for a later algorithm. The logic is done chiefly in the __call__ method, which calls the transition table.

from typing import Callable, Union

class SheeptalkFSA:
    """A Finite State Automaton for Sheeptalk"""

    def __init__(
        self,
        Q: set = {"q0", "q1", "q2", "q3", "q4"}, 
        sigma: set = {"a", "b", "!"}, 
        q0: str = "q0", 
        F: set = {"q4"}, 
        delta: Callable = delta  # defined above
    ):
        """Rename FSA parameters into readable variables"""
        self.states = Q
        self.inputs = sigma
        self.init_state = q0
        self.last_states = F
        self.delta = delta

    def __call__(self, q, i) -> Union[str, None]:
        """Run the transition table over the inputs"""
        return self.delta(q, i)

    def is_last_state(self, q) -> bool:
        """Check if current state is last state"""
        return q in self.last_states

You can cross-check the __init__ function to an FSA’s formal definition. Aside from the variable name change, they should map one to one. For example, we can use this class as follows:

fsa = SheeptalkFSA()            # create an instance
q_prime = fsa(q="q0", i="b")    # returns "q1"
fsa.is_last_state(q_prime)      # returns False

FSAs for recognition

FSAs help recognize if a given string (often called the input tape) is an instance of the automaton’s language. We do that through an algorithm called D-RECOGNIZE (short for “deterministic recognizer”).

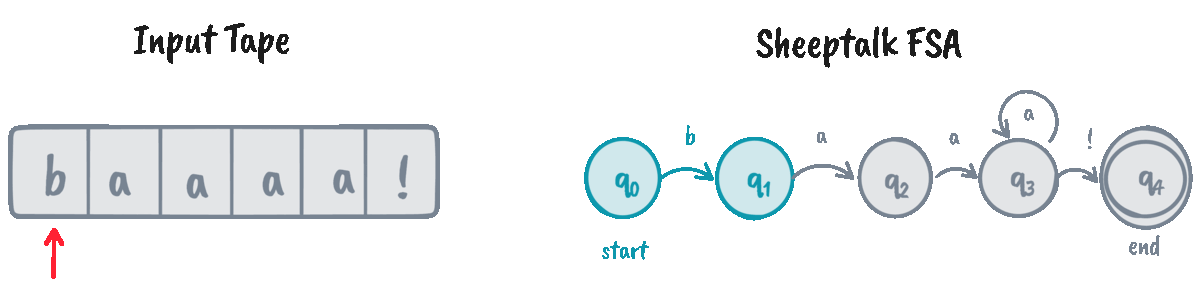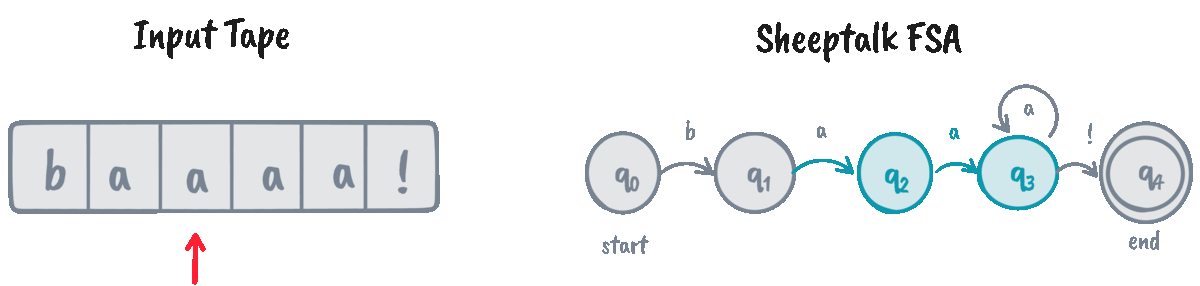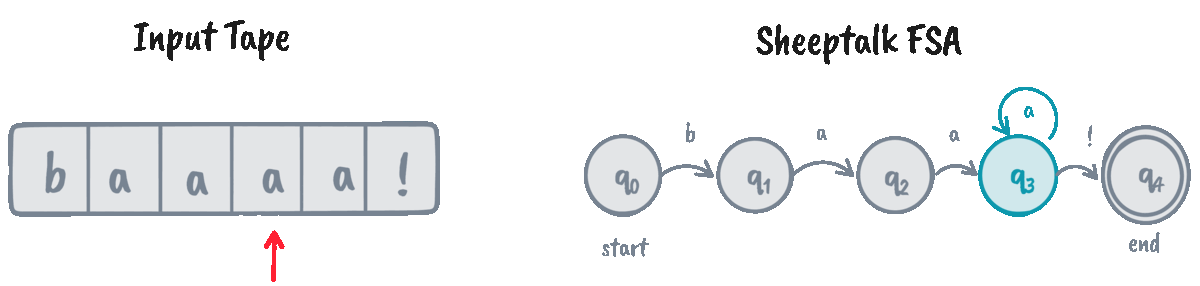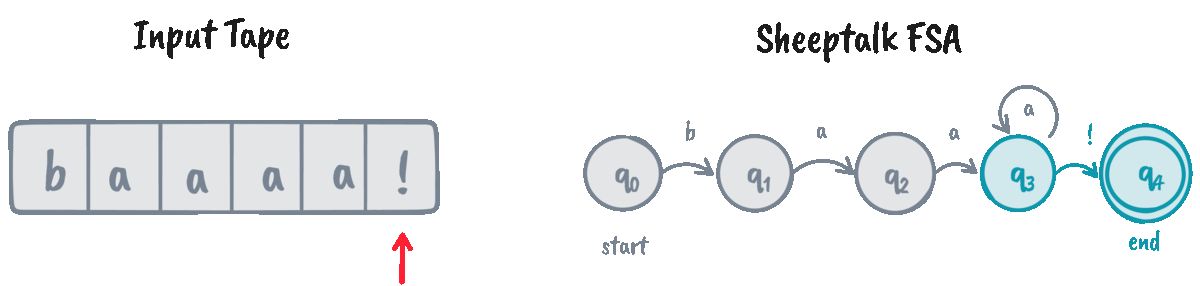
D-RECOGNIZE takes an input tape and an FSA as its arguments and returns an “accept” or “reject” result. I think it’s easier to show the pseudocode than explain the algorithm in words, so here’s a function implementing it:

def d_recognize(tape: str, machine: object) -> bool:
    index = 0  # beginning of tape
    current_state = machine.init_state

    while True:
        if index == len(tape):
            if machine.is_last_state(current_state):
                return True
            else:
                return False
        elif not machine(current_state, tape[index]):
            return False
        else:
            print(f"{index} | q: {current_state}, i: {tape[index]}")
            current_state = machine(current_state, tape[index])
            index += 1

This algorithm is a line-by-line translation of the pseudocode given in Jurafsky et al.’s Speech and Language Processing book. The function d_recognize returns True for “accept” and False for “reject.” Let’s now test our implementation on some input strings!

>>> machine = SheeptalkFSA()
>>> d_recognize("baaaaa!", machine)  # Returns True
| q: q0, i: b
| q: q1, i: a
| q: q2, i: a
| q: q3, i: a
| q: q3, i: a
| q: q3, i: a
| q: q3, i: !
>>> d_recognize("baa!", machine)  # Returns True
| q: q0, i: b
| q: q1, i: a
| q: q2, i: a
| q: q3, i: !
>>> d_recognize("baaaa", machine)  # Returns False
| q: q0, i: b
| q: q1, i: a
| q: q2, i: a
| q: q3, i: a
| q: q3, i: a
>>> d_recognize("meow!!", machine)  # Returns False

We can see that the algorithm traverses the whole tape and decides to “accept” the input if we arrive at the final state \(q_4\) at the end of the input. However, for cases like baaaaa, the FSA is stuck indefinitely at \(q_3\), causing the algorithm to ultimately “reject” it.

How does this relate to linguistics?

Finite state automata is a good way to understand word structure or morphology. As a motivating example, consider the FSA below:

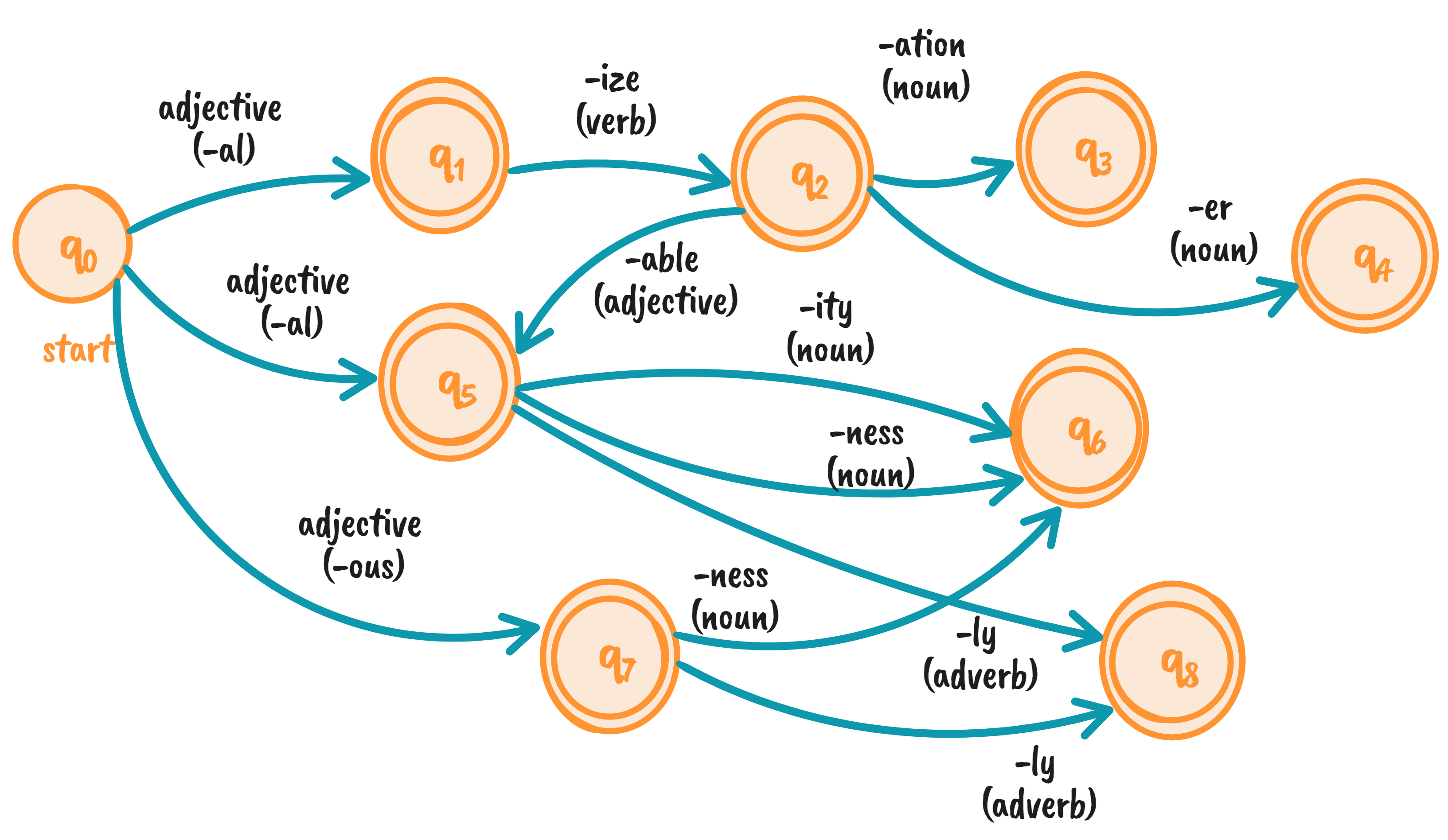
Observe how the symbols in our finite state automaton aren’t single characters. They can be strings or an entire ruleset. Each state, except for \(q_0\), can be a final state. The transition arcs represent rules for modifying an adjective, turning them into another part of speech. The three arcs leaving \(q_0\) show types of adjectives that end in a particular way (e.g., “-al”, “-ous”).

Let’s say we have an adjective, international. It ends with “-al,” meaning it transitioned through \(q_1\) or \(q_5\). If we take the first route, we can turn international into a verb by changing the suffix to “-ize,” that is, internationalize (\(q_2\)). We can go further and derive a noun by appending “-ation,” resulting in internationalization (\(q_3\)).

FSAs are good recognizers

We just applied orthographic rules on a word to modify it. The FSA above is a fragment of all the rules in the English language—and we’ve only touched adjectives. Aside from orthographic rules, we also have morphological rules that describe corner cases when modifying a word (e.g., irregular nouns).

If the Sheeptalk FSA allowed us to recognize words that belong to sheep-talk, then the FSA above enables us to determine whether an input string of letters is a legitimate English word or not. We refer to this task as morphological recognition.

Recognition is just one part of an NLP task known as morphological parsing. FSAs are particularly effective at recognition, especially when the state machine is robust. However, it cannot generate strings nor understand a word’s structure. Its only output is to accept or reject. We want something more complex for this task, like a Finite State Transducer (FST). I will cover FSTs in a later blog post.

Final thoughts

In this blog post, we looked into regular expressions (regex) through a linguistic lens. First, we learned that regexes describe a finite state automaton, which can characterize certain aspects of language. We then went through an example using Sheeptalk and showed an FSA’s formal definition alongside a code implementation. Then, we looked into the D-RECOGNIZE algorithm that allows us to recognize a text as an instance of that FSA.

Lastly, we also extended our view of FSAs by putting orthographic rules in our transition arcs, allowing us to “model” fragments of the English morphology. Similar to the Sheeptalk FSA identifying sheep talk, this new FSA can recognize if a text is a legitimate English word. For now, all FSAs can do is recognize strings. More complex tasks are done by a different mathematical model, i.e., the finite state transducer (FST).

I find FSAs to be the building blocks for understanding morphological parsing. It’s not yet the exciting part. In a later blog post, I will talk about FSTs, an extension of this concept. With FSTs, we can do morphological parsing, a highly relevant NLP task nowadays.

Footnotes

Technically, FSAs can only characterize formal languages (known as regular languages), which are quite different from natural languages. However, certain aspects of most natural languages, like morphology, belong to the set of regular languages. You can check out the chart below to see how each concept relates to the other:

↩